Feature extraction(특성 추출)
- 주성분 분석(Priciple Component Analysis, PCA)을 사용한 비지도(unsupervised) 데이터 압축
- 지도(superviesd) 방식의 차원 축소 기법인 선형 판별 분석(Linear Discriminant Analysis, LDA)을 이용하여 클래스 구별 능력 최대화
- 커널 PCA(Kernel Principle Component Analysis, KPCA)를 사용한 비선형 차원 축소
주성분 분석을 통한 비지도 데이터 압축
특성 추출은 새로운 특성 공간으로 데이터를 변화하거나 투영한다.(특성 선택과 특성 추출은 원본 특성 유지 하는가의 차이점이 있다.)
차원 축소 관점에서는 특성 추출은 대부분의 관련있는 정보를 유지하면서 데이터를 압축하는 방법이다.
특성 추출은 저장 공간을 절약하거나, 학습 알고리즘의 계산 효율성을 향상할 뿐 아니라, 차원의 저주문제도 감소시킨다.
규제가 없는 모델로 작업할 때, 효과적으로 예측 성능을 향상시킬 수 있는 도구가 된다.
주성분 분석(PCA)는 탐색적 데이터 분석, 주식 거래 시장의 잡음 제거,
생물정보학 분야에서 게놈(genome) 데이터나 유전자 발현(gene expression) 분석 등이 있다.
PCA는 특성 사이의 상관관계를 기반으로 데이터에 있는 특성을 잡아낼 수 있다.
고차원 데이터에서 분산이 가장 큰 방향을 찾고, 좀 더 작거나 같은 수의 차원을 갖는 새로운 부분 공간으로 이를 투영한다.
(새로운 부분 공간의 직교 좌표(주성분principal component)가 분산이 최대인 방향으로 해석)
Process of Principal component anlysis
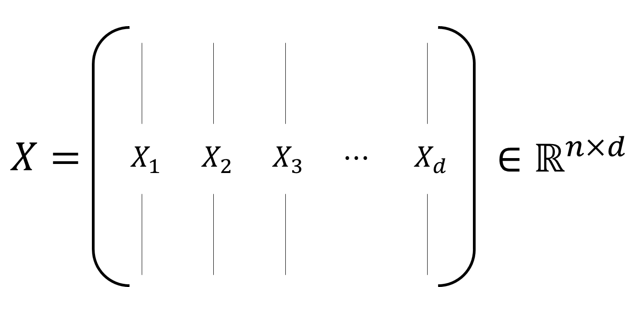
원본 특성 x(matrix_1Xd)와 변환 행렬W(matrix_dXk)로 투영을 이용해서
z(matrix_1Xk)를 얻을 수 있다.(k<<d)
첫 번째 주성분이 가장 분산이 크고, 다른 주성분들은 서로 직교한다는 제약하에 가장 큰 분산을 가진다.
PCA 방향은 데이터 스케일에 매우 민감하다.
특성 스케일이 다르고, 모든 특성의 중요도를 동일하게 취급하려면 PCA를 적용하기 전에 특성을 표준화 처리해야 한다.
1. d 차원 데이터셋을 표준화 전처리한다.
2. 공분산 행렬(covariance matrix)를 만든다.
3. 공분산 행렬을 고유 벡터(eigen vector)와 고유값(eigen value)로 분해한다.
4. 고윳값을 내림차순으로 정렬하고 그에 해당하는 고유 벡터의 순위를 매긴다.
5. 교윳값이 가장 큰 k 개의 고유 벡터를 선택한다. 여기서 k는 새로운 특성 부분 공간의 차원(k<=d)
6. 최상위 k개의 고유 벡터로 투영 행렬(projection matrix) W를 만든다.
7. 투영 행렬 W를 사용해서 d 차원 입력 데이터셋 X를 새로운 k 차원의 특성 부분 공간으로 변환한다.
고유벡터(eigenvector)는 그 행렬이 벡터에 작용하는 주축(principal axis)의 방향을 나타낸다.
공분산 행렬의 고유 벡터는 데이터가 어떤 방향으로 분산되어 있는지를 나타낸다.

주성분 추출 단계(1-4) with Wine data
1. 데이터 전처리(표준화)
import pandas as pd
df_wine=pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/wine/wine.data', header=None)
from sklearn.model_selection import train_test_split
X, y=df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test=\
train_test_split(X,y,test_size=0.3, stratify=y, random_state=0)
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
X_train_std=sc.fit_transform(X_train)
X_test_std=sc.fit_transform(X_test)
2. 공분산 행렬, 3. 고유값 고유행렬

공분산 행렬
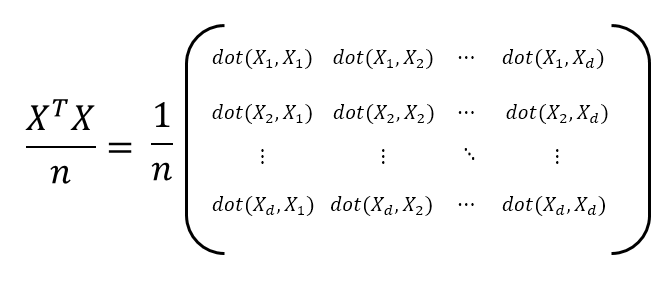 분산
분산(표준화 해주었기 떄문에 샘플 평균은 0)
공분산 행렬의 고유 벡터는 주성분(최대 분산의 방향)을 표현한다.
(분산이 최대가 되는 w를 찾는 문제는 공분산 행렬의 가장 큰 고윳값에 해당하는 벡터 w를 찾는 문제와 같다.)
이에 대응하는 고유값은 주성분의 크기를 표현한다.
넘파이의 linalg.eig 함수를 이용하면, 고유 벡터와 고유값을 구할 수 있다.
numpy.cov를 이용하면, 표준화 전처리된 훈련 데이터셋의 공분산 행렬을 계산한다.
import numpy as np
cov_mat=np.cov(X_train_std.T)
eigen_vals, eigen_vecs=np.linalg.eig(cov_mat)
print('\n고유값 \n%s' %eigen_vals)
고유값
[4.84274532 2.41602459 1.54845825 0.96120438 0.84166161 0.6620634
0.51828472 0.34650377 0.3131368 0.10754642 0.21357215 0.15362835
0.1808613 ]
numpy.linalg
numpy.linalg.eig 함수를 이용해서 대칭, 비대칭, 정방 행렬(square matrix) 모두 다룰 수 있지만,
이따금 복소수 고윳값을 반환한다.
numpy.linalg.eigh 함수는 에르미트 행렬을 분해, 공분산 행렬과 같은 대칭 행렬을 다룰 때,
수치적으로 더욱 안정된 결과를 만든다. 항상 실수 고윳값을 반환
참고)
사이킷런 PCA 클래스는 직접 고윳값과 고유 벡터를 계산하는 대신
특이값 분해(singular value decompostion) 방식을 사용하여 주성분을 구한다.
singular_values_ 속성을 사용해서 특이값을 얻을 수 있다.
4. 순서 정렬(내림차순)
가장 많은 정보(분산)를 가진 고유 벡터(주성분) 일부만 선택한다.
고유값은 고유 벡터의 크기를 결정하므로 고윳값을 내림차순으로 정렬한다.(k 개)
설명된 분산 비율(explained variance ratio)
고유값의 설명된 분산 비율은 전체 고윳값의 합에서 해당 고윳값의 비율이다.
tot=sum(eigen_vals)
var_exp=[(i/tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp=np.cumsum(var_exp)
import matplotlib.pyplot as plt
plt.bar(range(1,14), var_exp, alpha=0.5, align='center', label='Individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid', label='Cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
bar // 막대 그래프
step // 분산의 누적합을 계산
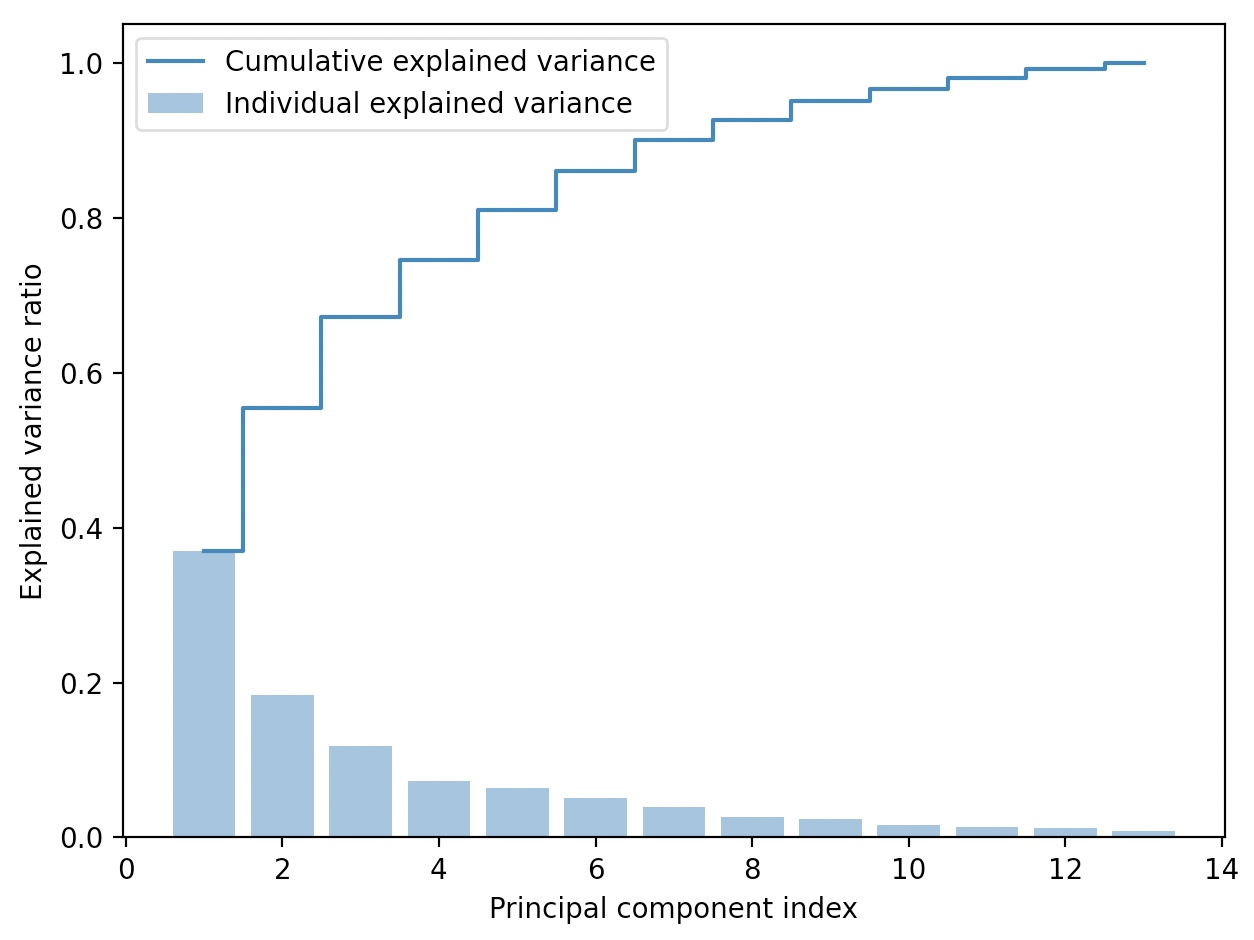
첫 번째 주성분이 거의 분산의 40%를 커버하고 있으며, 처음 두개의 주성분이 데이터셋에 있는 분산의 60% 설명
분산 그래프가 랜덤 포레스트 특성 중요도와 유사하지만, PCA는 비지도 학습이다.
클래스 레이블에 관한 정보를 사용하지 않는다.
특성변환(5-8)
5. 고유벡터 선택(차원) 6. 투영 행렬
(고유값, 고유벡터) 튜플의 리스트 생성, 내림차순으로 정렬
eigen_pairs=[(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]
eigen_pairs.sort(key=lambda k:k[0], reverse=True)
가장 큰 두 개의 고유값에 해당하는 고유 벡터를 선택(분산의 약 60%를 잡아낼 수 있다.)
두 개의 벡터를 이용한 투영 행렬 생성
w=np.hstack((eigen_pairs[0][1][:, np.newaxis], eigen_pairs[1][1][:, np.newaxis]))
print('투영 행렬:\n', w)
[[-0.13724218 0.50303478]
[ 0.24724326 0.16487119]
[-0.02545159 0.24456476]
[ 0.20694508 -0.11352904]
[-0.15436582 0.28974518]
[-0.39376952 0.05080104]
[-0.41735106 -0.02287338]
[ 0.30572896 0.09048885]
[-0.30668347 0.00835233]
[ 0.07554066 0.54977581]
[-0.32613263 -0.20716433]
[-0.36861022 -0.24902536]
[-0.29669651 0.38022942]]
8. 투영행렬을 사용한 차원 변환
X_train_std[0].dot(w)
array([2.38299011, 0.45458499])
124X13차원의 훈련 데이터셋 두 개의 주 성분으로 투영(124X2로 변환)
X_train_pca=X_train_std.dot(w)
colors=['r', 'b', 'g']
markers=['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train==l, 0], X_train_pca[y_train==l, 1], c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
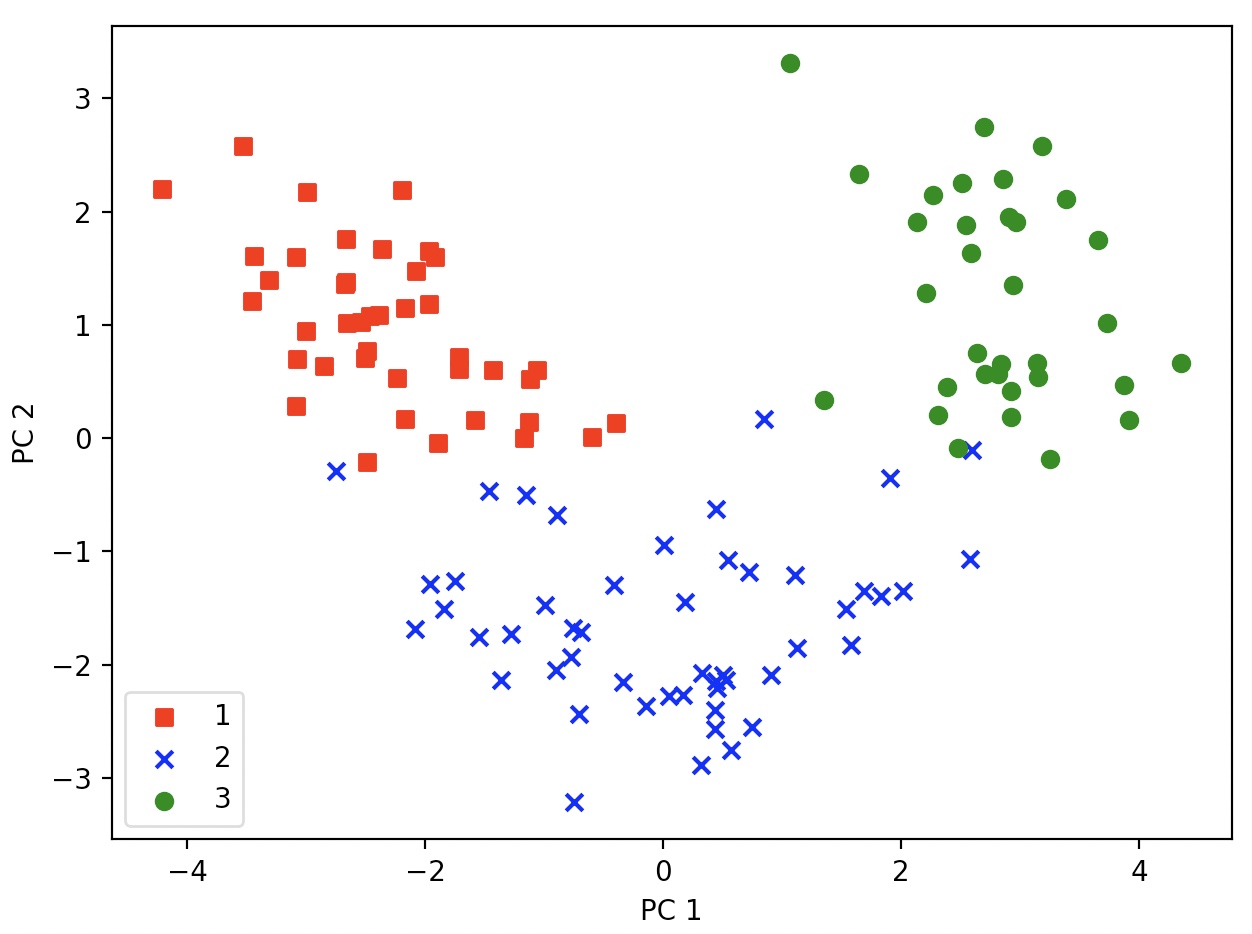
산점도를 그리기 위한 목적으로 클래스 레이블을 사용했을 뿐,
PCA는 어떤 클래스 레이블 정보도 사용하지 않는 비지도 학습 기법이다.
PCA with Scikit-learn
PCA는 scikit-learn의 변환기 클래스 중 하나이다.
훈련 데이터를 사용하여, 모델을 훈련하고 같은 모델 파라미터를 사용하여
훈련 데이터셋과 테스트 데이터셋을 변환한다.
PCA 클래스로 Wine 데이터셋의 훈련 데이터셋에 적용하고, 로지스틱 회귀로 변환된 샘플 데이터를 분류
##decision_regions drawing function
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X,y, classifier, test_idx=None, resolution=0.02):
markers=('s','x','o', '^','v')
colors=('red','blue','lightgreen','gray','cyan')
cmap=ListedColormap(colors[:len(np.unique(y))])
x1_min,x1_max=X[:,0].min()-1, X[:,0].max()+1
x2_min,x2_max=X[:,1].min()-1, X[:,1].max()+1
xx1,xx2=np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
Z=classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
Z=Z.reshape(xx1.shape)
plt.contourf(xx1,xx2,Z,alpha=0.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y==cl, 0],y=X[y==cl,1],alpha=0.8, c=colors[idx], label=cl, edgecolor='black', marker=markers[idx])
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
lr=LogisticRegression(random_state=1)
X_train_pca=pca.fit_transform(X_train_std)
X_test_pca=pca.transform(X_test_std)
lr.fit(X_train_pca, y_train)
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

고유 벡터는 음수나 양수 부호를 가질 수 있기 때문에 위와 거울에 비친 것처럼 뒤집힌 경우도 있다.
테스트 데이터셋 결정 경계
plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legned(loc='lower left')
plt.tight_layout()
plt.show()

전체 주성분의 설명된 분산 비율을 알고 싶다면, n_components 매개변수를 None으로 지정하고 PCA 클래스의 객체를 만들면 된다.
(None으로 지정하였기 때문에 차원 축소를 수행하는 대신 분산의 크기 순서대로 모든 주성분이 반환된다.)
explained_variance_ratio_ 속성에서 모든 주성분의 설명된 분산 비율을 확인할 수 있다.
pca=PCA(n_components=None)
X_train_pca=pca.fit_transform(X_train_std)
pca.explained_variance_ratio_
array([0.36951469, 0.18434927, 0.11815159, 0.07334252, 0.06422108,
0.05051724, 0.03954654, 0.02643918, 0.02389319, 0.01629614,
0.01380021, 0.01172226, 0.00820609])
n_components에 (0, 1)사이 실수를 입력하면 비율을 나타낸다.
pca=PCA(n_components=0.95)
print('주성분의 개수:',pca.n_components_)
print('설명된 분산 비율:', np.sum(pca.explained_variance_ratio))
실행 불가
n_components=‘mle’로 지정하면 토마스 민카(Thomas Minka)가 제안한 차원 선택 방식을 사용한다.
pca=PCA(n_components='mle')
print('주성분의 개수:', pca.n_components_)
print('설명된 분산 비율:', np.sum(pca.explained_variance_ratio_))
실행 불가
IncrementalPCA
PCA는 배치로만 실행되기 때문에 대용량 데이터셋을 처리하려면 많은 메모리가 필요하다.
IncrementalPCA를 사용하면 데이터셋의 일부를 사용하여 반복적으로 훈련할 수 있다.
partial_fit() 메서드는 네트워크나 로컬 파일 시스템으로부터 조금씩 데이터를 받아서 훈련할 수 있다.
fit() 메서드는 numpy.memmap을 사용하여 로컬 파일로부터 데이터를 조금씩 읽어 올 수 있다.
한번에 읽어올 데이터의 크기는 IncrementalPCA 클래스의 batch_size로 지정한다.
default 값은 특성 개수의 5배
IncrementalPCA의 n_components 매개변수는 정수 값만 입력할 수 있다.
from sklearn.decomposition import IncrementalPCA
ipca=IncrementalPCA(n_components=9)
for batch in range(len(X_train_std)//25+1):
X_batch=X_train_std[batch*25:(batch+1)*25]
ipca.partial_fit(X_batch)
print('주성분 개수:', ipca.n_components_)
print('설명된 분산 비율:', np.sum(ipca.explained_variance_ratio_))
주성분 개수: 9
설명된 분산 비율: 0.9478392700446676